Distribusi Probabilitas Kontinu Menggunakan R Part 2

Distribusi Chi2 dengan satu derajat kebebasan

Ini adalah distribusi X^2, jika variabel acak X mengikuti distribusi gaussian standar.

curve(dchisq(x,1), xlim=c(0,5), col='red', lwd=3)
abline(h=0,lty=3)
abline(v=0,lty=3)
title(main="Chi2, one degree of freedom")

Distribusi Chi2 dengan n derajat kebebasan

Ini adalah distribusi probabilitas dari X1^2+...+Xn^2, di mana variabel acak X1, X2, ..., Xn adalah gaussian standar independen.

Kami memenuhi distribusi ini dalam statistik, ketika melakukan perhitungan yang membutuhkan varians populasi, tanpa mengetahui varians ini: kami menggantinya dengan varians sampel.

Kita akan membahas ini secara lebih mendalam ketika kita menangani estimator dan uji statistik.

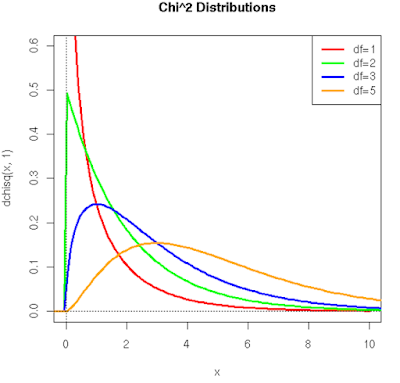
curve(dchisq(x,1), xlim=c(0,10), ylim=c(0,.6), col='red', lwd=3)
curve(dchisq(x,2), add=T, col='green', lwd=3)
curve(dchisq(x,3), add=T, col='blue', lwd=3)
curve(dchisq(x,5), add=T, col='orange', lwd=3)
abline(h=0,lty=3)
abline(v=0,lty=3)
legend(par('usr')[2], par('usr')[4], xjust=1,
       c('df=1', 'df=2', 'df=3', 'df=5'),
       lwd=3,
       lty=1,
       col=c('red', 'green', 'blue', 'orange')
      )
title(main='Chi^2 Distributions')

Student's T

Jika X1, X2, X3,... adalah variabel acak gaussian berdistribusi identik bebas harapan mu dan standar deviasi sigma, maka

  X1 + X2 + ... + Xn
 --------------------  -  mu
          n
-----------------------------
          sigma
        ---------
         sqrt(n)

Mengikuti hukum gaussian. Tetapi jika kita mengganti simpangan baku dengan simpangan baku sampel (yaitu, penaksir simpangan baku populasi), besaran ini tidak lagi mengikuti distribusi gaussian tetapi distribusi Student T dengan (n-1) derajat kebebasan.

curve( dt(x,1), xlim=c(-3,3), ylim=c(0,.4), col='red', lwd=2 )
curve( dt(x,2), add=T, col='blue', lwd=2 )
curve( dt(x,5), add=T, col='green', lwd=2 )
curve( dt(x,10), add=T, col='orange', lwd=2 )
curve( dnorm(x), add=T, lwd=3, lty=3 )
title(main="Student T distributions")
legend(par('usr')[2], par('usr')[4], xjust=1,
       c('df=1', 'df=2', 'df=5', 'df=10', 'Gaussian distribution'),
       lwd=c(2,2,2,2,2), 
       lty=c(1,1,1,1,3),
       col=c('red', 'blue', 'green', 'orange', par("fg")))

F Fisher

Jika X1, X2, ... Xn dan Y1, Y2, ... Ym saling bebas berdistribusi identik dengan variabel acak gaussian, maka

  X1^2 + X2^2 + ... + Xn^2
 --------------------------
            n
----------------------------
  Y1^2 + Y2^2 + ... + Ym^2
 --------------------------
            m

mengikuti distribusi F, dengan n dan m derajat kebebasan. Ini adalah distribusi hasil bagi variabel Chi2 independen, masing-masing dibagi dengan derajat kebebasannya.

Kami akan memenuhi distribusi ini ketika kami membandingkan varians (misalnya, dalam Anova (Analysis Of VAriance) atau dalam uji statistik).

curve(df(x,1,1), xlim=c(0,2), ylim=c(0,.8), lty=2)
curve(df(x,3,1), add=T)
curve(df(x,6,1), add=T, lwd=3)
curve(df(x,3,3), add=T, col='red')
curve(df(x,6,3), add=T, lwd=3, col='red')
curve(df(x,3,6), add=T, col='blue')
curve(df(x,6,6), add=T, lwd=3, col='blue')
title(main="Fisher's F")
legend(par('usr')[2], par('usr')[4], xjust=1,
       c('df=(1,1)', 'df=(3,1)', 'df=(6,1)', 
         'df=(3,3)', 'df=(6,3)', 
         'df=(3,6)', 'df=(6,6)'),
       lwd=c(1,1,3,1,3,1,3),
       lty=c(2,1,1,1,1,1,1),
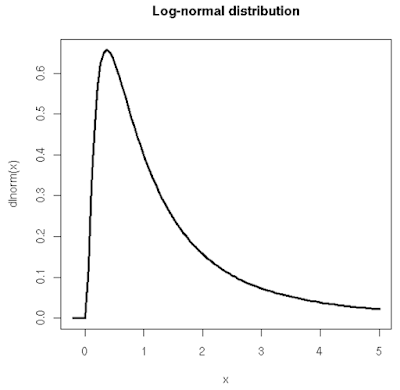
       col=c(par("fg"), par("fg"), par("fg"), 'red', 'red', 'blue', 'blue'))

Hukum lognormal

Cukup sering, variabel yang kita temui di dunia nyata memiliki nilai positif: dengan variabel yang benar-benar gaussian, ini tidak mungkin -- kita tahu bahwa variabel kita bukan gaussian. Sebagai gantinya, kita dapat melihat apakah logaritma ots adalah gaussian -- dengan kata lain, jika variabel kita adalah eksponensial dari variabel gaussian.

curve(dlnorm(x), xlim=c(-.2,5), lwd=3,
      main="Log-normal distribution")

Cauchy

Ini adalah contoh distribusi yang tersebar secara patologis: variansnya tidak terbatas.

Kadang-kadang disebut distribusi pemanah: seorang pemanah yang ditutup matanya, di depan dinding yang tak terbatas menembakkan panah ke arah yang acak. Distribusi dampak panah di dinding adalah distribusi Cauchy.

N <- 100                         # Number of arrows
alpha <- runif(N, -pi/2, pi/2)   # Direction of the arrow
x <- tan(alpha)                  # Arrow impact
plot.new()
plot.window(xlim=c(-5, 5), ylim=c(-1.1, 2))
segments( 0, -1,     # Position of the Bowman
          x, 0   )   # Impact
d <- density(x)
lines(d$x, 5*d$y, col="red", lwd=3 )
box()
abline(h=0)
title(main="The bowman's distribution (Cauchy)")
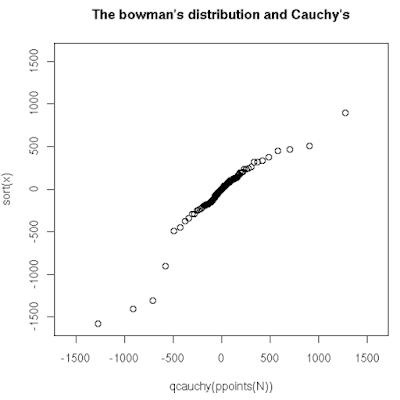
# Exercise: turn this into an animation...

N <- 10000
x <- tan(runif(N, -pi/2, pi/2))
xlim <- qcauchy(2/N)
xlim <- c(xlim, -xlim)
plot(qcauchy(ppoints(N)),  sort(x),
     xlim=xlim, ylim=xlim,
     main="The bowman's distribution and Cauchy's")

Ini juga merupakan kasus pembatas dari distribusi Student T, dengan 1 derajat kebebasan.

curve(dcauchy(x),xlim=c(-5,5), ylim=c(0,.5), lwd=3)
curve(dnorm(x), add=T, col='red', lty=2)
legend(par('usr')[2], par('usr')[4], xjust=1,
       c('Cauchy distribution', 'Gaussian distribution'),
       lwd=c(3,1),
       lty=c(1,2),
       col=c(par("fg"), 'red'))