1. Definisi Analisis Factor
Analisis faktor adalah sebuah teknik yang digunakan untuk mencari faktor-faktor yang mampu menjelaskan hubungan atau korelasi antara berbagai indikator independen yang diobservasi. Analisis faktor merupakan perluasan dari analisis komponen utama. Analisis faktor digunakan untuk mengidentifikasi sejumlah faktor yang relatif kecil yang dapat digunakan untuk menjelaskan sejumlah besar variabel yang saling berhubungan. Sehingga variabel-variabel dalam satu faktor mempunyai korelasi yang tinggi, sedangkan korelasi dengan variabel-variabel pada faktor lain relatif rendah. Tiap-tiap kelompok dari variabel mewakili suatu konstruksi dasar yang disebut faktor. Untuk meningkatkan daya interpretasi faktor, harus dilakukan transformasi pada matriks loading. Transformasi dilakukan dengan merotasi matriks tersebut dengan metode varimax, quartimax, equamax, quartimin, biquartimin dancovarimin serta oblimin.
2. Tujuan Analisis Faktor
Tujuan utama analisis faktor adalah untuk menjelaskan struktur hubungan di antara banyak variabel dalam bentuk faktor atau vaiabel laten atau variabel bentukan. Faktor yang terbentuk merupakan besaran acak (random quantities) yang sebelumnya tidak dapat diamati atau diukur atau ditentukan secara langsung. Berikut adalah tujuan lainnya
Untuk mereduksi sejumlah variabel asal yang jumlahnya banyak menjadi sejumlah variabel baru yang jumlahnya lebih sedikit dari variabel asal, dan variabel baru tersebut dinamakan faktor atau variabel laten atau konstruk atau variabel bentukan.
Untuk mengidentifikasi adanya hubungan antarvariabel penyusun faktor atau dimensi dengan faktor yang terbentuk, dengan menggunakan pengujian koefisien korelasi antarfaktor dengan komponen pembentuknya. Analisis faktor ini disebut analisis faktor kofirmatori.
Untuk menguji valisitas dan reliabilitas instrumen dengan analisis faktor konfirmatori.
Validasi data untuk mengetahui apakah hasil analisis faktor tersebut dapat digeneralisasi ke dalam populasinya, sehingga setelah terbentuk faktor, maka peneliti sudah mempunyai suatu hipotesis baru berdasarkan hasil analisis faktor.
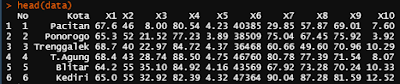
Kita kali ini akan melakukan analisis faktor pada data kesehatan penduduk di Jawa Timur. Tujuannya nanti akan didapatkan faktor baru yang dapat merepresentasikan variabel-variabel penyusun indeks kesehatan penduduk di Jawa Timur.
|
No
|
Kota
|
X1
|
X2
|
X3
|
X4
|
X5
|
X6
|
X7
|
X8
|
X9
|
X10
|
|
1
|
Pacitan
|
67.6
|
46
|
8
|
80.54
|
4.23
|
40385
|
29.85
|
57.87
|
69.01
|
7.6
|
|
2
|
Ponorogo
|
65.3
|
52
|
21.52
|
77.23
|
3.89
|
38509
|
75.04
|
67.45
|
75.92
|
3.92
|
|
3
|
Trenggalek
|
68.7
|
40
|
22.97
|
84.72
|
4.37
|
36468
|
60.66
|
49.6
|
70.96
|
10.29
|
|
4
|
T.Agung
|
68.4
|
43
|
28.74
|
88.5
|
4.75
|
46760
|
80.78
|
77.39
|
71.54
|
8.07
|
|
5
|
Blitar
|
64.2
|
55
|
35.1
|
84.92
|
4.16
|
43569
|
67.92
|
73.28
|
70.24
|
10.33
|
|
6
|
Kediri
|
65
|
55
|
32.92
|
82.39
|
4.32
|
47364
|
90.04
|
87.28
|
81.59
|
12.52
|
|
7
|
Malang
|
66.4
|
55
|
24.96
|
83.88
|
4.11
|
42213
|
81.39
|
81.82
|
74.7
|
19.31
|
KeteranganVariabel:
X1 : Angka Harapan Hidup (th)
X2 : Angka Kematian Bayi (bayi/1000 kelahiran hidup)
X3 : Presentase Keluhan Kesehatan (%)
X4 : Presentase Angka Melek Huruf (%)
X5 : Rata-rata Lama Sekolah (th)
X6 : Pengeluaran Rata-rata Perkapita (ribu)
X7 : Prosentase Rumah Tangga Pemakai Listrik (%)
X8 : Prosentase Rumah Tangga dengan Sumber Air Minum Bersih (%)
X9 : Prosentase Rumah Tangga dengan Dinding Tembok Kayu (%)
X10 : Prosentase Rumah Tangga dengan Luas Lantai Perkapita (≤10m2 (%))
Diatas merupakan sample data yang digunakan, untuk lengkapnya bisa download
DISINI.
Kita terlebih dahulu meng-copy data yang berada di Microsoft Excel yang akan dimasukkan kedalam program R, setelah kita meng-copy datanya, lalu ketikkan syntax berikut:
#Panggildata
data <- read.delim("clipboard") #membaca data yang di copy
head(data) #untuk melihat head data
Untuk menangani data missing, salah satu cara yang dapat digunakan adalah menghapus baris data yang memuat missing dengan syntax:
# Menghapus row data yang kosong atau missing
databaru <- na.omit(data)
summary(databaru)
Setelah kita melihat summary data, selanjutnya mendeteksi data outlier. Sebelum mendeteksi data outlier, kita mengambil data yang akan dideteksi outlier nya terlebih dahulu dengan mengetikkan syntax berikut:
library(MVN)
hasil=mvOutlier(databaru, qqplot=T, method="quan")
Plot tersebut menunjukkan bahwa terdapat 11 data yang termasuk kedalam data outlier dari total data berjumlah 37 data.
Untuk menangani data outlier, cara yang dapat digunakan adalah menghapus baris data yang memuat outlier dengan cara ketikkan syntax:
newdata=hasil$newData
Lalu kita juga dapat melihat summary data tanpa data missing dan outlier.
summary(newdata)
Sebelum kita melakukan uji KMO dan uji Barlett, terlebih dahulu membuat fungsi sebagai berikut.

Selanjutnya, kita dapat menghitung korelasi, lakukan uji KMO dan Uji Barlett. Syntax nya adalah:
cor(newdata)
Output diatas menunjukkan bahwa matriks diagonal korelasi selalu bernilai 1 karena variabel tersebut berkorelasi dengan dirinya sendiri sehingga nilai korelasinya adalah 1. Misalkan diambil contoh korelasi antara X2 (Angka kematian bayi) dan X1 (Angka harapan hidup) nilai korelasinya adalah -0,8580975. Hubungan yang terbentuk antara X2 dan X1 bersifat negatif dan lemah, artinya semakin tinggi tingkat angka harapan hidup maka kemungkinan untuk angka kematian bayi tersebut akan semakin rendah. Jika diambil contoh lagi antara X5 (rata-rata lama sekolah) dan X4 (persentase angka melek huruf) nilai korelasinya adalah 0,9270303. Hubungan yang terbentuk adalah positif dan kuat, yang artinya semakin tinggi lama sekolah, maka kemungkinan persentase angka melek huruf juga semakin tinggi
kmo(newdata)
Berikut uji hipotesis yang dilakukan untuk uji bartlett :
1.Hipotesis
H0: Data tidak terdapat korelasi dari semua pertanyaan
H1: Paling sedikit terdapat satu korelasi
2.Signifikasi
α: 0.05
3.Daerah kritis
H0 ditolak jika P-value < α
4.Statistik Uji
P-value = 2.2x10-16
5.Keputusan
Karena nilai p-value (2.2x10-16) < nilai α (0.05), maka tolak H0
6.Kesimpulan
Dengan tingkat signifikansi 0.05, maka dapat disimpulkan bahwa pada data tersebut paling sedikit terdapat satu korelasi.
uji_bart(newdata)

Berikut uji hipotesis yang dilakukan untuk uji KMO:
1.Hipotesis
H0: Data tidak cukup untuk difaktorkan
H1: Data cukup untuk difaktorkan
2.Signifikasi
α: 0.05
3.Daerah kritis
H0 ditolak jika p-value < α
4.Statistik Uji
Nilai keseluruhan p-value > 0.05
5.Keputusan
Karena nilai p-value(0,731437) > nilai α(0,05), maka gagal tolak H0
6.Kesimpulan
Dengan tingkat signifikansi 0.05, maka dapat disimpulkan bahwa data tersebut tidak cukup untuk difaktorkan.
Selanjutnya analisis factor varimax dengan memanggil paket library(pysch) dan ketikkan syntax:
pcadata <- principal(newdata,nfactor=2,rotate="varimax",scores=T)
pcadata
Dilihat dari output tersebut, komponen yang terbentuk ada 2 komponen. Proportion variance untuk PC1 adalah sebesar 0,59. Artinya faktor pertama mampu menjelaskan variansi dari 10 variabel sebesar 59%. Kemudian faktor kedua (PC2) mampu menjelaskan variansi dari keseluruhan variabel yang diamati sebesar 18%.
Selanjutnya, untuk melihat plot kompnen data yang terbentuk yaitu dengan cara mengetikkan syntax sebagai berikut:
plot(pcadata$values,type="b",ylab="Nilai Eigenvalues",xlab="Komponen yang terbentuk",lab=c(5,5,5))
Mungkin sekian untuk post kali ini thank you
 Reviewed by Jimmy Pujoseno
on
November 16, 2020
Rating:
Reviewed by Jimmy Pujoseno
on
November 16, 2020
Rating:





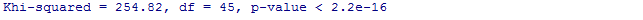








Bang kok fungsi mvoutlier tidak ditemukan ya kenapa? Apa ada yg kurang?
ReplyDeletecoba install mvn versi 4.0. bisa cek ini https://www.rdocumentation.org/packages/MVN/versions/4.0/topics/mvOutlier
Delete