Analisis gerombol (analisis cluster) merupakan teknik peubah ganda yang mempunyai tujuan utama untuk mengelompokkan objek-objek berdasarkan kemiripan karakteristik yang dimilikinya. Karakteristik objek-objek dalam suatu kelompok memiliki tingkat kemiripan yang tinggi, sedangkan karakteristik antar objek pada suatu kelompok dengan kelompok lain memiliki tingkat kemiripan yang rendah. Dengan kata lain, keragaman dalam suatu gerombol minimum sedangkan antar keragaman antar gerombol maksimum. Kemiripan antar objek diukur dengan menggunakan ukuran jarak. Beberapa ukuran jarak yang sering digunakan antara lain jarak Euclid, jarak mahalanobis, jarak City-block (Manhattan), dan lain-lain (Mattik dan Sumertajaya, 2011)
K-means adalah algoritma pembelajaran mesin tanpa pengawasan yang digunakan untuk menemukan kelompok pengamatan (cluster) yang memiliki karakteristik yang sama. Apa arti dari pembelajaran tanpa pengawasan? Ini berarti bahwa pengamatan yang diberikan dalam kumpulan data tidak diberi label, tidak ada hasil yang dapat diprediksi.
Kami akan menggunakan set data Wine untuk mengelompokkan berbagai jenis anggur. Set data ini berisi hasil analisis kimia anggur yang ditanam di daerah tertentu di Italia. Anda bisa download disini.
1. Memuat data
Pada kode baris 2-5 kami memanggil packages yang dibutuhkan kemudian memanggil data wine pada kode 8 dengan fungsi read.csv(). Setelah itu kita tampilkan 6 row data menggunakan fungsi View(head()). Kemudian setelah itu kita akan menghapus kolom ke 14 yaitu Customer_Segment.
Dari output diatas dapat dilihat bahwa terdapat 14 kolom dimana kolom terakhir yaitu Customer_Segment. Kami tidak menggunakan kolom Customer_Segment, seperti yang telah kami katakan sebelumnya, k-means adalah algoritma pembelajaran mesin tanpa pengawasan dan bekerja dengan data yang tidak berlabel.
Dari output diatas dapat dilihat bahwa terdapat 14 kolom dimana kolom terakhir yaitu Customer_Segment. Kami tidak menggunakan kolom Customer_Segment, seperti yang telah kami katakan sebelumnya, k-means adalah algoritma pembelajaran mesin tanpa pengawasan dan bekerja dengan data yang tidak berlabel.
2. Explore Data
Pertama kita harus mengeksplorasi dan memvisualisasikan data untuk melihat data yang kita punya seperti apa apakah terdapat penyimpangan-penyimpangan.
Pada kode baris kedua kita akan melihat output struktur dari data yang kita punya. Dari struktur dapat dilihat bahwa terdapat 178 observasi (row) dan 13 Variabel (kolom). Kita juga dapat melihat type dari data yang kita punya diantaranya ada numerik dan int.
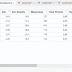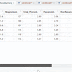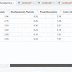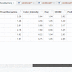
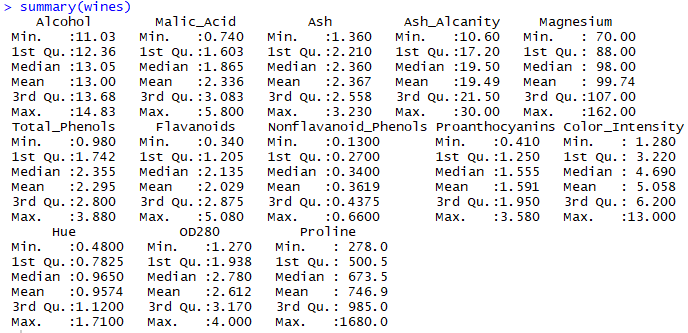
Semua kolom dinyatakan sebagai angka atau bilangan bulat. Bagaimana dengan distribusi statistik?. Kita akan melihat statistik deskriptif dari data menggunakan kode baris ke-5. Pada output deskriptif, nilai masing masing variabel berbeda beda mulai dari minimum hingga maksimum. Misalnya pada variabel Alcohol didapat nilai minimum adalah 11.03 sedangkan pada variabel Proline 278. Begitu juga dengan nilai maksimumnya jauh berbeda. Kita bisa lihat menggunakan histogram juga untuk melihat deskriptif dari data menggunakan kode baris 8-13.
Dari Histogram diatas juga kita bisa lihat deskriptif dari variabel terkait frekuensi dan value masing - masing variabel. Misal pada Variabel Alkohol kita melihat bahwa data yang ada memiliki frekuensi dibawah 20.
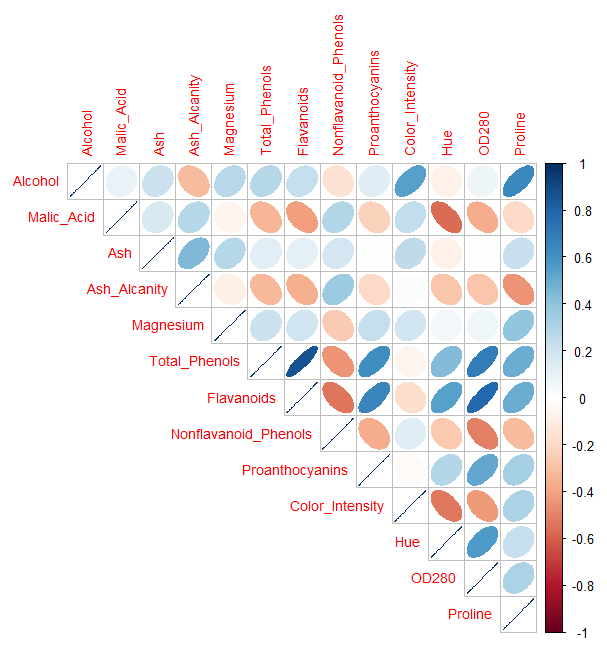
Apa hubungan antara variabel yang berbeda? Kita dapat menggunakan fungsi corrplot () pada kode baris 16 untuk membuat tampilan grafis dari matriks korelasi sehingga kita bisa melihat korelasi dari masing variabel. dari output diatas dapat kita lihat bahwa semakin biru warnanya maka semakin kuat hubungan(positif) antara kedua variabel tersebut contohnya Total_Phenois dan Flavanoids. Sebaliknya apabila semakin Merah maka hubungan (negatif) antara kedua variabel semakin kuat seperti variabel Malic_Acid dengan Hue. Apabila berwarna putih maka dapat dikatakan tidak ada hubungan antara kedua variabel sebagai contoh variabel Ash dan OD280
Semua kolom dinyatakan sebagai angka atau bilangan bulat. Bagaimana dengan distribusi statistik?. Kita akan melihat statistik deskriptif dari data menggunakan kode baris ke-5. Pada output deskriptif, nilai masing masing variabel berbeda beda mulai dari minimum hingga maksimum. Misalnya pada variabel Alcohol didapat nilai minimum adalah 11.03 sedangkan pada variabel Proline 278. Begitu juga dengan nilai maksimumnya jauh berbeda. Kita bisa lihat menggunakan histogram juga untuk melihat deskriptif dari data menggunakan kode baris 8-13.
Dari Histogram diatas juga kita bisa lihat deskriptif dari variabel terkait frekuensi dan value masing - masing variabel. Misal pada Variabel Alkohol kita melihat bahwa data yang ada memiliki frekuensi dibawah 20.
Apa hubungan antara variabel yang berbeda? Kita dapat menggunakan fungsi corrplot () pada kode baris 16 untuk membuat tampilan grafis dari matriks korelasi sehingga kita bisa melihat korelasi dari masing variabel. dari output diatas dapat kita lihat bahwa semakin biru warnanya maka semakin kuat hubungan(positif) antara kedua variabel tersebut contohnya Total_Phenois dan Flavanoids. Sebaliknya apabila semakin Merah maka hubungan (negatif) antara kedua variabel semakin kuat seperti variabel Malic_Acid dengan Hue. Apabila berwarna putih maka dapat dikatakan tidak ada hubungan antara kedua variabel sebagai contoh variabel Ash dan OD280
Ada korelasi linear yang kuat antara Total_Phenols dan Flavanoids. Kita dapat memodelkan hubungan antara dua variabel ini dengan memasang persamaan linear seperti pada kode baris 19-21. Dari output persamaan linear dapat dilihat persebaran data antara kedua variabel mengikuti garis lurus atau dapat dikatakan linear.
Sekarang setelah kita melakukan explorasi data, kita akan menyiapkan data untuk menjalankan algoritma k-means.
3. Menyiapkan Data
Kita harus menormalkan variabel untuk mengekspresikannya dalam rentang nilai yang sama. Dengan kata lain, normalisasi berarti menyesuaikan nilai yang diukur pada skala yang berbeda ke skala umum. Seperti yang kami sebutkan diatas bahwa memang masing masing variabel memiliki rentang yang berbeda (max,min) sehingga perlu disetarakan atau normalisasi.
Kode diatas akan kita gunakan untuk membandingkan data real dan data setelah normalisasi. Dari output diatas dapat dilihat bahwa titik-titik dalam data yang dinormalkan sama dengan yang asli. Satu-satunya hal yang berubah adalah skala sumbu.
4. K-means Clustering
Di bagian ini kita akan menjalankan algoritma k-means dan menganalisa komponen utama yang mengembalikan fungsi.
Fungsi kmean () mengembalikan objek kelas "kmean" dengan informasi tentang partisi:
Cluster : Sebuah vektor bilangan bulat (dari 1: k) menunjukkan cluster yang dialokasikan setiap titik.
Centers : Sebuah matriks pusat klaster.
Size : Jumlah poin di setiap cluster.
Baris kode 4 yaitu kode untuk melakukan cluster kmeans. Kemudian kode baris 7,10,13 masing masing menunjukkan nilai Cluster Centers dan size.
Baris kode 4 yaitu kode untuk melakukan cluster kmeans. Kemudian kode baris 7,10,13 masing masing menunjukkan nilai Cluster Centers dan size.
Dari output diatas dapat dilihat terdapat 2 cluster kemudian terdapat juga nilai centers dari masing masing variabel dan size dari cluster.
Selain itu, fungsi kmean () mengembalikan beberapa rasio yang memberi tahu kita betapa ringkasnya cluster dan bagaimana perbedaan beberapa kelompok di antara mereka sendiri.
Selain itu, fungsi kmean () mengembalikan beberapa rasio yang memberi tahu kita betapa ringkasnya cluster dan bagaimana perbedaan beberapa kelompok di antara mereka sendiri.
- Betweens, Jumlah kuadrat antar cluster. Dalam segmentasi yang optimal, seseorang mengharapkan rasio ini menjadi setinggi mungkin, karena kami ingin memiliki cluster yang heterogen.
- Withinss, Vektor jumlah kuadrat dalam cluster, satu komponen per cluster. Dalam segmentasi yang optimal, seseorang mengharapkan rasio ini serendah mungkin untuk setiap cluster, karena kami ingin memiliki homogenitas dalam cluster.
- Tot.withinss, Total jumlah kuadrat dalam cluster
- Tots, Jumlah total kuadrat.
Didapatkan nilai Betweens, Withinss, Tot.withinss dan tots dari output program di atas seperti gambar dibawah ini.
5. Banyak Cluster
Untuk mempelajari secara grafis nilai mana dari k yang memberikan kita partisi terbaik, kita dapat memplot betweens dan tot.withinss vs k yang dipilih.
Yang merupakan nilai optimal untuk k? Seseorang harus memilih sejumlah kluster sehingga menambahkan cluster lain tidak memberikan partisi data yang jauh lebih baik. Pada titik tertentu, gain akan turun, memberikan sudut pada grafik (kriteria siku). Jumlah cluster dipilih pada titik ini. Dalam kasus kami, jelas bahwa 3 adalah nilai yang sesuai untuk k.
6. Result
Dari output diatas kita dapat lihat mean dari masing masing grup cluster.
Dalam entri ini kita telah belajar tentang algoritma k-means, termasuk normalisasi data sebelum kita menjalankannya, pilihan jumlah cluster yang optimal (kriteria siku) dan visualisasi pengelompokan. Untuk full code bisa kunjungi my github disini.
Thank You sudah berkunjung jangan lupa komen dan follow blognya terimakasih
Clustering Data Menggunakan K-means
 Reviewed by Jimmy Pujoseno
on
July 13, 2018
Rating:
Reviewed by Jimmy Pujoseno
on
July 13, 2018
Rating:
 Reviewed by Jimmy Pujoseno
on
July 13, 2018
Rating:
Reviewed by Jimmy Pujoseno
on
July 13, 2018
Rating:














You should see how my pal Wesley Virgin's story begins with this shocking and controversial video.
ReplyDeleteYou see, Wesley was in the army-and shortly after leaving-he unveiled hidden, "MIND CONTROL" secrets that the CIA and others used to obtain whatever they want.
THESE are the exact same methods many celebrities (especially those who "come out of nowhere") and the greatest business people used to become wealthy and famous.
You probably know how you use less than 10% of your brain.
That's really because the majority of your brainpower is UNTAPPED.
Maybe this thought has even taken place INSIDE your very own brain... as it did in my good friend Wesley Virgin's brain around 7 years back, while driving an unlicensed, beat-up trash bucket of a car without a license and $3.20 on his debit card.
"I'm absolutely frustrated with going through life paycheck to paycheck! When will I get my big break?"
You've been a part of those those questions, ain't it right?
Your success story is waiting to start. You just have to take a leap of faith in YOURSELF.
CLICK HERE TO LEARN WESLEY'S SECRETS